東海地区大会において山口先生が正多角形
の一筆書きの方法を紹介された。
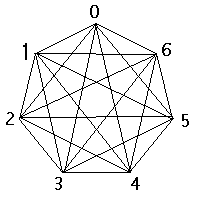
例 正七角形
正七角形の頂点を0,1,2,3,4,
5,6とする。
対角線の数=7C2=21本である。
書き方 対角線の長さは(7−1)/2=3
種類あるから、


西三数学サークル通信37号
正n角形の一筆書き・・・・・・・・梶田(岡崎東高校)
| 昨年の12月に名古屋で行われた数教協 東海地区大会において山口先生が正多角形 の一筆書きの方法を紹介された。 例 正七角形 正七角形の頂点を0,1,2,3,4, 5,6とする。 対角線の数=7C2=21本である。 書き方 対角線の長さは(7−1)/2=3 種類あるから、 |
 |
 |
一筆書きを利用した壁掛け |
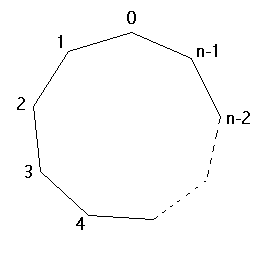
| 一般に、正n角形(nは奇数とする) の一筆書きは正n角形の頂点を0, 1,2,3・・・n-1とする。 2点を結ぶ線分はnC2=n(n-1)/2 本あり、対角線の同じ長さの線分は (n-1)/2 種類ある。 |
 |
下のように線を引いていく。
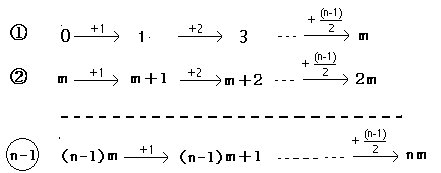
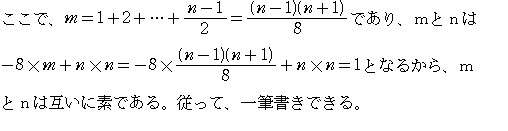
トレミーの定理を復習すると三角関数
の加法定理が見えてくる・・・中村(刈谷高校)
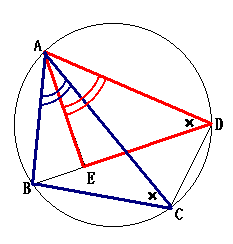
| トレミーの定理 四角形ABCDが円に内接するならば AB・CD+BC・DA=AC・BD 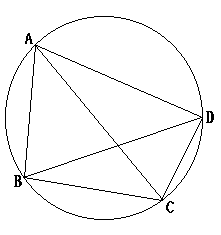 |
トレミーの定理の証明
1 2
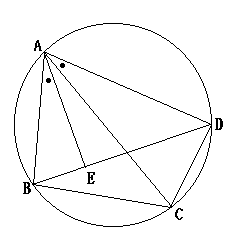
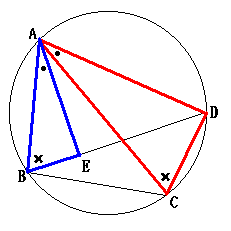
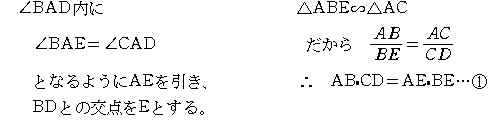
3 4

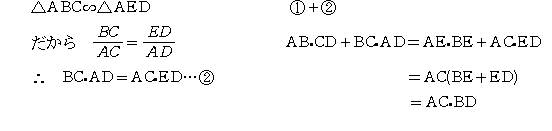
ここから第2の山場
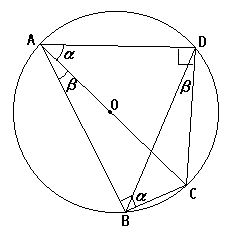 |
ここで、あらためて円Oに内接する □ABCDを考える。(右図) AO=0.5 AC(直径)=1 とすると、∠ACD=∠ABC=90°だから DC=sinα AD=cosα BC=sinβ AB=cosβ DB=sin(α+β) (∵△ABDで正弦定理をつかう) そこで、トレミーの定理により(←いよいよ使います!) AC・DB=AB・DC+AD・BC すなわち 1×sin(α+β)= cosβ×sinα+cosα×sinβ ∴ sin(α+β)=sinαcosβ+cosαsinβ |
※ トレミーの定理は逆(□ABCDにおいて AB・CD+AD・BC=AC・BD ならば、
この□ABCDは円に内接する)も成り立つ。
※ トレミーは天文学者プトレマイオスの英語読みです。つまり、同一人物。